UJI FISHER (FISHER EXACT TEST)

Uji Fisher merupakan suatu tehnik untuk menganalisa data diskrit (nominal atau ordinal) ketika dua sampel independen adalah kecil.  Skor dibuat dalam bentuk frekuensi dalam tabel kontingensi 2 x 2  seperti berikut ini:
 

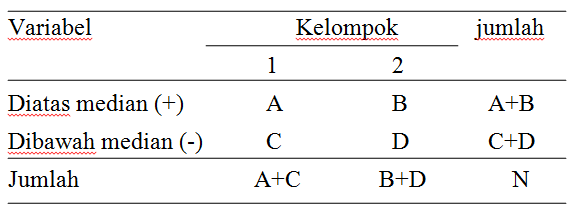
Peluang (probabilita) untuk pemunculan frekuensi-frekuensi pada table 2 x 2 ketika  jumlah marginal fixed adalah dengan distribusi hypergeometric sebagai berikut:

 

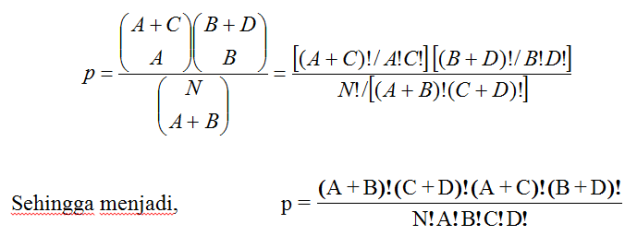
Untuk mendapatkan p-value ketika H₀ benar , kita harus menjumlahkan probabilita dari pemunculan data dengan probabilita dari kemungkinan pemunculan yang lebih ekstrim.
Hipotesis:
H₀ : P₁ = P₂.
H₁ : P₁ ≠ P₂ (untuk uji dua arah) atau
P₁ > P₂ atau P₁ < P₂ (untuk uji satu arah)
Gunakan formula hypergeometric untuk mendapatkan nilai probabilita (p-value) (atau anda dapat menggunakan tabel Fisher, lihat pada buku nonparametric statistics karangan Sidney Siegel dan N. John Castellan, Jr.).  Jika  p-value < α  maka keputusannya adalah tolak H₀.   jika  N > 15  gunakan uji χ² (seperti pada uji median)
Contoh: berikut adalah 12 observasi dari dua kelompok data yang dibagi dalam dua kategori yaitu diatas median dan dibawah median.  Ujilah apakah proporsi diatas media populasi I lebih besar dari populasi II?  Gunakan α = 0,05.


Keputusan:      Tolak H₀ karena  p-value < α
Kesimpulan:    proporsi diatas median populasi I lebih besar dari populasi II dengan  tingkat keyakinan sebesar 95%.
Untuk uji dua arah
Ho :  P₁ = P₂
H1 :  P₁ ≠ P₂
Peluang tersebut diatas ditambah dengan kemungkinan pemunculan ekstrim dari sisi yang lain.
Kemungkinan pemunculan yang lebih ekstrim dari sisi yang lain


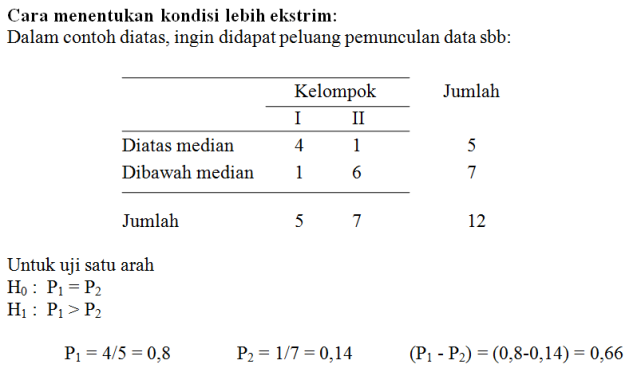
Setiap kemungkinan pemunculan yang mempunyai selisih peluang (P₁ – P₂) lebih besar dari 0,66 maka dikatakan mempunyai peluang pemunculan yang lebih ekstrim.
Untuk uji dua arah
H₀ :  P₁ = P₂
H1 :  P₁ ≠ P₂
peluang pemunculan yang lebih ekstrim juga berlaku untuk arah yang berlawanan.